Oracle Penalty Method
The oracle penalty method is an advanced approach for constraint handling for evolutionary and metaheuristic optimization algorithms. The method is based on a single parameter Omega (Ω), which is called an oracle due to its predictive nature. This parameter directly corresponds to the global optimal objective function value f(x). In case of real-world applications where the user has some (rough) guess about a possible global optimal f(x) value, this information can be exploited as oracle information to improve the convergence speed of the optimization algorithm. In case no such user guided information is available, an (automated) update rule can be applied for Ω, starting with a value of infinity (∞) and updating Ω after individual optimization runs, when better (feasible) solutions have been found. Algorithms implementing the oracle penalty method with automated update are classified as self-tuning. The oracle penalty method has been applied for example in Ant Colony Optimization (ACO) see [1], [6], [7], [15], [17], Genetic Algorithms (GA) see [2], [10], [11], Particle Swarm Optimization (PSO) see [3],[16], Artificial Bee Colony Algorithm see [12] and Differential Evolution (DE) see [4], [5], [8], [13] and was also extended to deterministic methods [14]. The most detailed introduction to the method can be found in [1], a brief motivation of the key idea of the method can be found in this PDF presentation (slide 11-15). The oracle penalty method is one of the major reasons why MIDACO is capable to solve problems with hundreds of (non-linear) constraints fast & robust (see Benchmarks).
Mathematical Formulation of the extended Oracle Penalty Function ( Section 2.3 )
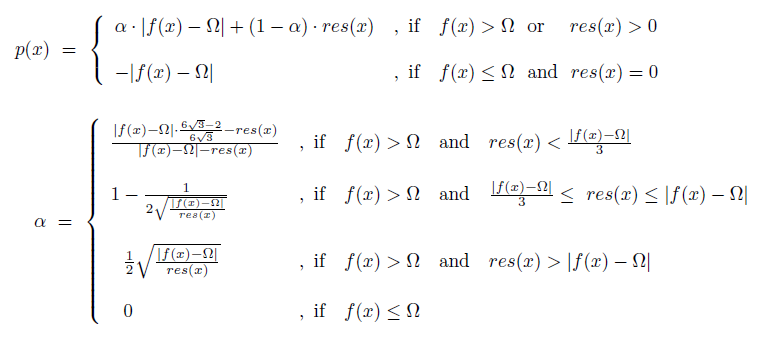
Graphical illustration of the extended oracle penalty function for Omega = 0
| Source code | ||
| Matlab | oracle_penalty.m |
LaTeX formula |
| C/C++ | oracle_penalty.cpp | |
| Fortran | oracle_penalty.f | |
| [1] | Schlueter, Gerdts |
The Oracle Penalty Method
|
Journal of Global Optimization (Springer), Vol. 47, Issue 2, Pages 293-325 (Preprint) (2010) |
| [2] | Munawar et al. | Advanced genetic algorithm to solve MINLP problems over GPU | IEEE Congress on Evolutionary Computation CEC, pp. 318 - 325 (link) (2011) |
| [3] | Dong, Cheng, Niu | A Constrained Particle Swarm Optimization Algorithm with Oracle Penalty Method | Applied Mechanics and Material (AMM) pp. 303-306, 1519 (2013) |
| [4] | Dong, Wang, Cheng, Jiang | Composite differential evolution with modified oracle penalty method for constrained optimization problems |
Mathematical Problems in Engineering, Vol. 1, pp. 1-15, DOI:10.1155/2014/617905 (Paper) (2014) |
| [5] | Dong, Cheng, Niu | Adaptive Constrained Differential Evolution Algorithms based on Oracle Penalty Function | Computer Applications and Software (Chinese), DOI:10.3969/j.issn.1000-386x.2014.01.078 (2014) |
| [6] | Gebreslassie, Diwekar | Efficient ant colony optimization for computer aided molecular design: case study solvent selection problem |
Computers & Chemical Engineering (Elsevier) Volume 78, Pages 1–9 (2015)
|
| [7] | Gebreslassie, Diwekar | Efficient ant colony optimization (EACO) algorithm for deterministic optimization | Int. J. Swarm Intel. Evol. Comput. 5:131. doi:10.4172/2090-4908.1000131 (link) (2016) |
| [8] | Chen, Liang | An Optimization Approach of SRM Sphere Slot Grain Design Based on Improved Differential Evolution Algorithm | Advanced Materials Research, Vol 971-973, Pages 1072-1075 (2014) |
| [9] | Gago-Vargas et al. | Nonlinear integer problems with applications to engineering design | Computational Optimization and Applications (Springer), http://dx.doi.org/10.1007/s10589-015-9739-3 (Preprint) (2015) |
| [10] | Sato, Watanabe, Igarashi |
Multimaterial Topology Optimization of Electric Machines Based on Normalized Gaussian Network |
IEEE Transaction on Magnetics, Vol. 51, No. 3, Art. 7202604 (Preprint) (2015) |
| [11] | Noguera |
What's New in DiscoverSim Version 2 |
INFORMS 2015 Workshop, Philadelphia USA (PPTX) (2015) |
| [12] | Zhang, Han, Wang |
Emulsion Explosive Formulation Optimization Based on Hybrid Artificial Bee Colony Algorithm |
Acta Analysis Functionalis Applicata, Vol.17, No.4, pp. 421-430 (Preprint) (2015) |
| [13] | Shi, Liu, Feng, Zhao |
Improved Differential Evolution Based PA Energy Efficiency Optimization Scheme with Joint Polarization-QAM in OFDM Systems |
IEEE/CIC International Conference on Communications in China (ICCC), DOI: 10.1109/ICCChina.2017.8330407 (link) (2017) |
| [14] | Costa, Rocha, Fernandes |
A Penalty Approach for Solving |
Springer Proceedings in Mathematics & Statistics, vol 223. doi.org/10.1007/978-3-319-71583-4_4 (link) (2018) |
| [15] | Paffrath, Zhou, Guo, Ertl |
Interactive winding geometry design of power transformers |
IEEE/ICOA, 4th Inter. Conf. on Opt. App., DOI: 10.1109/ICOA.2018.8370494 (link) (2018) |
| [16] | Zhengtonga, Zhengqi, Xiaokui, Chen |
Multimaterial layout optimization of truss structures via an improved particle swarm optimization algorithm |
Computers & Structures, Vol. 222, pp 10-24 (Elsevier) (2019) |
| [17] | Acciarini |
Solar Sailing Polar Mission to the Sun |
Master Thesis, TU-Delft, Netherlands (link) (2019) |
| [18] | Sato, Igarashi |
Automatic Design of PM Motor Using Monte Carlo Tree Search |
IEEE Transaction on Magnetics, DOI: 10.1109/TMAG.2022.3164926, (link) (2022) |
| [19] | Otomo, Sato, Ken, Onozaka, Hajime |
Parameter and Topology Optimizations for Wireless Power Transfer Device |
IEEE Transactions on Magnetics, DOI: 10.1109/TMAG.2023.3301995 (link) (2023) |
